What this is
An in depth perspective on how blockchain and cryptocurrencies work, along with a running commentary on social value, libertarianism, and whatever the heck fits my fancy. I’m attempting to write this at a high school comprehension level so that those who haven’t sat through 4 years of computer engineering classes can make sense of all of this.
What this isn’t
A primer on Bitcoin, an economic treatise, or a how-to. (Although, elements of all of those things will appear)
For those who don’t feel like scrolling through pages and pages of my ramblings, here’s the TL;DR. Blockchain is a bunch of messages with security built into them. The security isn’t perfect, but each message is increasingly secure as time passes. The list of messages is saved on every computer that participates in the blockchain, and the lists are constantly being compared for agreement. Blockchain relies on a bit of a gambit. They essentially say “you may be able to break the security on one node, or even a few, but after a few the increased security that comes with time passing will catch up with you, and you’ll be stuck well before you come close to succeeding in fraud.”
A Survey of Computer Science
Numbers in an Array
Computers are complex and simple at the same time. It takes millions of lines of code and tens of thousands of man-hours to put together the latest Windows or OSX version, and yet everything a computer does is simply a whole bunch of numbers saved in an array called memory.
Let’s look at an example computer memory:

Let’s ignore all of the writing for a moment and discuss what we’re looking at. Memory is “byte-addressable,” which means that you can access information 8 bits (there are 8 bits in a byte; a bit is a single value of “1” or “0”) at a time. If I want to access the byte at address 0, I write some code that properly references address 0, and I have access to the value in that address of memory. If all data was 8 bits long (e.g. a number between 0 and 255), then we’d have a pretty easy go of accessing data. Just remember the order you put it in, and you just call the number that you put it in (minus 1 because the addresses start at 0).
However, as shown in the above image, data can be much larger than 8 bits. The yellow 2-byte data is a short integer (e.g. a value between 0 and 65,535). The purple 4-byte data is an integer (e.g. a value between 0 and ~4.3 billion). There are other types of data that are even longer, like decimal numbers (called floating point numbers). Here’s more info on memory and how it works. Now it gets a bit more complicated to remember where things are in memory.
Arrays: A Simple Way to Store Large Amounts of Data
When dealing with simple data, like an integer, storing it in memory is relatively simple. As long as you know what address it starts at and how long that type of data is, you can access and retrieve the data. However, what are we to do when there is a bunch of related data?
For example, what if we want to store the daily profits for the week from our monocle and top hat shop? Now we don’t have just one piece of data to deal with, but seven. We could just toss each day’s profit into memory as we encounter it, but the accounting program we’re running may store additional info in memory: temporary values, user credentials, and other information needed by the program will also reside in memory.
We can remember each address for each individual day’s profit data, but these values are related, and it’s hard to manage access information on seven values, let alone 70 or 700 or 700,000. Treating each value individually doesn’t scale.
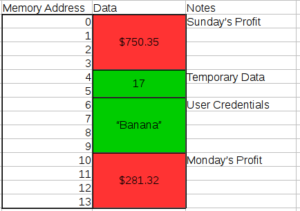
As shown above, Sunday’s Profit is separated from Monday’s Profit (both in red) by intervening unrelated data (in green). In order to access the week’s profit, you need to know the address of each and every day’s profit, and you have to individually retrieve each data point.
In comes a better way to handle such data: Arrays! Much like memory is an array with addresses referencing each byte, array data structures store related information sequentially so that each piece of information can be referenced with an array address.
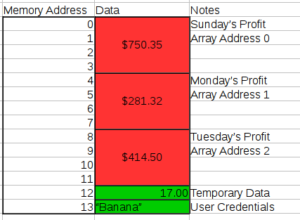
The difference is clear. The array groups the related data together, and you can simply reference the array to get to any of the data. Array address 0 is Sunday’s profit, which is located in memory addresses 0-3. Array address 1 is Monday’s Profit and is located in memory addresses 4-7. Rather than needing to remember all of the memory addresses for each day’s profit, you can simply remember the starting memory address of the array, and use the array address to calculate where each piece of information in the array is located. For example, array address 1 translates to the array starting memory address (0) plus one array element (which is 4 bytes long), resulting in a memory address of 4. If you look at the above image, array address 1 starts at memory address of 4. NOTE: I haven’t included all 7 days of profit in the above image so that it won’t get too complicated and confusing. Here is some additional information on arrays.
However, you can also see a limitation in the above image. It works great if you know exactly how much data you need to store, but look at where the Temporary Data and User Credentials are stored. If you need to include one more piece of information in the array, you’re hosed. Either you have to start moving a bunch of stuff around in memory to make room (which is not ideal), or you have to continue the array somewhere else in memory and keep track of 2 array portions (which is also not ideal).
Linked Lists: Good for dynamic data
You may be wondering what the point of all of this is. We’re talking about blockchain, not about memory management, right? I promise, this is where we connect to blockchain.
Let’s see if we can combine the best of both worlds. Writing each day’s profit to memory separately allows you to add additional days without having to shuffle data around in the memory. On the other hand, preserving the relationship between all of the days’ profits without having to keep track of each day’s memory address allows you to scale up to large amounts of data without overcomplicating things.
One of the “best of both worlds” solutions is called a linked list. A linked list operates much like writing each day’s profit to memory separately, but preserves the relationship between the different days by including an additional bit of information pointing to the location of another day’s profit in memory.
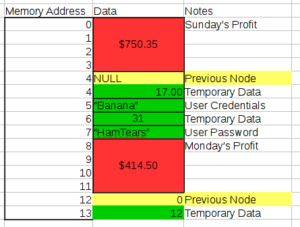
As you can see, we have expanded Sunday’s profit and Monday’s profit from 4 bytes to 5 bytes. The additional byte (in yellow) points to the previous node. Since Sunday’s profit is the first node, its previous node is NULL (meaning it doesn’t have a previous node). Since Monday’s profit is the second node, it points back to Sunday’s profit. Previous Node 0 points to the starting memory address of Sunday’s profit.
Visualized another way, the linked list looks like this:

This is the basis of blockchain. A data structure with a payload and a reference to the previous block in the chain. Now let’s talk about security.
Hashes: Breakfast for the Masses
I dunno about y’all, but I’m sick of reading. Let’s take a quick break before getting into hashes by enjoying some pictures

Breakfast Hash and some red meat for the audience.


Hashes: Preserving Relationships and Security
Alright, back out of your bunks. Time for some more learnin’. Hashes are conceptually simple, but mathematically complicated. Since we’re not diving into the math, this section should be a breeze!

No, not that kind of Brees!
Let’s take a look at the array again:

If we call Array[0] we get Sunday’s Profit, and if we call Array[1] we get Monday’s profit. However, we don’t always have a situation where we know exactly what order the data will be put into the array. Imagine, for a moment, that instead of 3 days of profits, we have 3 years of profits, entered manually by an employee who isn’t guaranteed to get everything perfectly in order. How do we find Monday’s Profit in that deluge of data?
The traditional way is to search for the data in the array. Here is some more information on searching.
The fun way is to use hashing! How about we use some relevant characteristic of the data to access the data instead of the array index (“index” is another term for array address number). All you need is two math equations: one to determine the hash from the data, and another to determine a memory location from the hash.
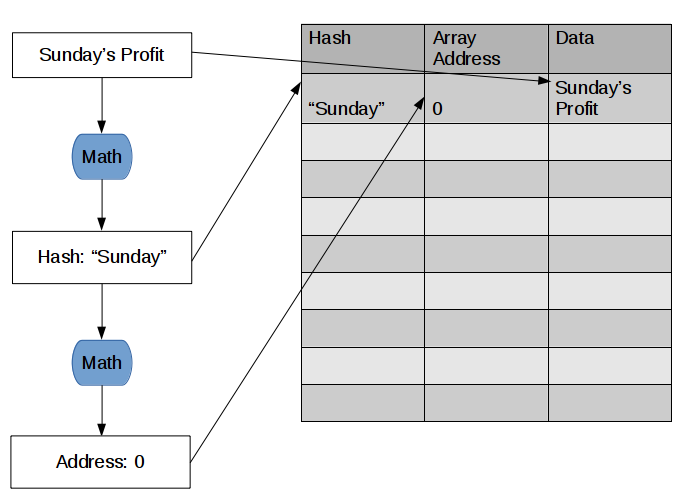
As you can see, Sunday’s Profit data was hashed to “Sunday”, which is a characteristic of the data (specifically, the day of the week), and “Sunday” was computed to be connected to array address 0. Now, instead of accessing Sunday’s Profit data by loading Array[0], you can access Sunday’s Profit data by loading HashArray[“Sunday”].
If this is a bit confusing, another simple hashing algorithm that appears in everyday life may clarify things. Placing medical records in alphabetical order by the first letter of the last name is another hashing algorithm. If the last name is SMITH, the “algorithm” for obtaining the hash involves looking at the first letter of the last name, “S”. Then, the hash “S” points to a specific shelf in the fileroom (the “S” shelf, for lack of a better name). SMITH’s folder is placed on the “S” shelf. When I want to retrieve a folder starting with “S”, I pull a folder off the “S” shelf, and I have SMITH’s folder.
But there are many people with a last name starting with “S”. What happens when SMITH’s folder is stored on the “S” shelf and I want to store Slaver’s folder? This is called a “hash collision.” Depending on the specific situation, a hash collision is either an inevitability or a disaster. In cases where hash collisions are expected, we could simply change the data stored. Rather than just storing one piece of data for each hashed value, we can store the data for each hash in a linked list. Now, the “S” shelf looks like this (pointer is just a fancy term for the memory address):
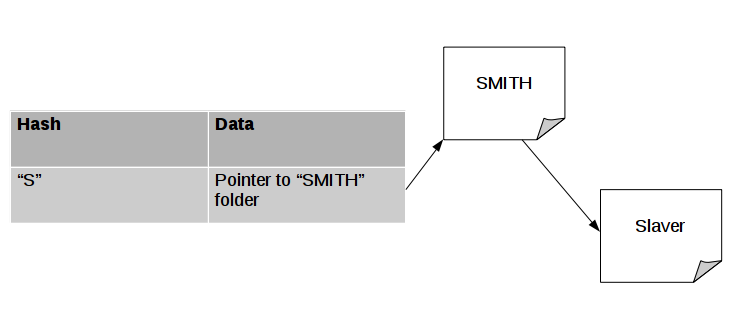
This is great for categorization hashes like the alphabetical sorting of medical records, but isn’t the best for cryptographic hashes like are used in blockchains. Instead, cryptographic hashes rely on another protection from hash collisions, small data density.
Bitcoin and most other cryptocurrencies use what is called SHA-256 hashing. In SHA-256, a message of any* size is hashed using really fancy math into a 256 bit number, which means there are 2^256 possible hashes (1.1×10^77 for you scientific notation folks, or roughly 1/10 of the total number of atoms in the universe). Hash collisions are so rare under SHA-256 as to be practically nonexistent.
*Technically, there is a maximum length of message, but it’s enormous.
But I mentioned above that hashes are based on characteristics of the data. “S” is the first letter of SMITH, and it’s fairly easy to see the relation. What is the relation between some seemingly random 256 digit number and a Bitcoin block? Well, it has to do with math well beyond my ken, but you can go here for a bit of an explanation (as well as a look ahead). In essence, the math takes all of the data, divides it into chunks, and does a mathematical transformation on each chunk before assembling the results into the hash.
Okay, assuming you’re following along so far, you understand how categorization hashes work and that cryptographic hashes are different, but how do cryptographic hashes work?
Cryptographic hashes work on the principle that it’s much easier to do the math to hash the data than to derive the data from the hash. Let’s look again at the medical records example for a picture of how this works. If you’re given the last name SMITH and told that the hashing function (fancy term for the math to calculate the hash) is the first letter of the last name. It’s trivial to calculate a hash of “S” from the data “SMITH.” However, let’s go the other direction… if all I give you is “S”, you have thousands of last names to choose from. The chance of you guessing “SMITH” is extremely low.
The same principle applies to SHA-256 hashes. It’s relatively easy for a computer to calculate the hash from the original data, but (practically) impossible to derive the original data from the hash.
We’ll discuss the specific way cryptographic hashes are used in blockchains later on.
Let’s take another break. Things are getting a bit intense. In the spirit of the glib baby pics from a while back, here’s me in a sombrero.

Cultural Appropriation from a Young Age
How about some relaxing pics from a backpacking trip I took a long time ago?


Public Key Cryptography
Alright, back to talking security! We’ve laid the groundwork for explaining the structure and security of the blocks in a blockchain, but let’s talk about individual currency transactions and how they’re secured. If I want to send 50 bitcoins to ZARDOZ, we create a transaction to transfer the bitcoins from my wallet to his. The details will be covered later, but it’s important to notice that without any security, STEVE SMITH could read the transaction, and use the information contained in the transaction to create a fake transaction to send the 50 bitcoins to him instead of ZARDOZ.
What sort of security is used on these transactions? Public key cryptography! Public key cryptography uses the same concept of “one way” algorithms, just like the cryptographic hashes. In fact, in some cases, the mathematics for generating cryptographic hashes is used in public key cryptography.
How does it work? Let’s assume I want to send a secret message to ZARDOZ. I’m sending it over the Internet, which isn’t a particularly trustworthy place. I can’t just send the text in the open. ZARDOZ decides to generate two “keys.” In this context, one of the keys is used in combination with fancy math to encrypt the message so that it can’t be read by STEVE SMITH. The other key is used in combination with more fancy math to decrypt the message. The cool thing about public key cryptography is that you can’t figure out the decrypting key by looking at the encrypting key or at an encrypted message. This is called asymmetric cryptography.
In contrast, symmetric cryptography can be “broken” by looking at the encryption key and the encrypted message. Of course, that means you shouldn’t broadcast your symmetric encryption key on an insecure channel. For example, if my encryption algorithm is addition of the encryption key to the data, and my encryption key is 4, then if my data is the number 10, the encrypted data is the number 14 (10+4 = 14). I send 14 across the unsecured network to ZARDOZ, who uses the symmetric decryption key (the number 4), and the decryption algorithm of subtraction of the decryption key from the data, and ZARDOZ gets the original data, the number 10 (14 – 4 = 10).
Seems secure enough, especially when we use something more complicated than “add 4” as an encryption. But why are we talking about asymmetric cryptography instead? Well, because we have a problem. The Internet isn’t particularly secure, and we’re not gonna VPN with the entire bitcoin network, most of whom we don’t trust, to send them our secret key. With asymmetric cryptography, the encryption key (called the public key) can be known by everybody. It doesn’t matter if half the world can encrypt messages intended for you. As long as they’re not able to decrypt those encrypted messages, the system is secure. That’s why the decryption key is called the private key. The private key must be kept secret by the receiver of the message.
As shown above, I have sent ZARDOZ the message “Molon Labe!” ZARDOZ has vomited forth (published) his public key, which allowed me to encrypt my message and send it across the Internet securely. As you can see, STEVE SMITH can try his hardest to intercept my message to ZARDOZ, but all he gets is a bunch of gibberish. Then, once ZARDOZ receives the encrypted message, he uses his private decryption key (secreted away in the Vortex where nobody can access it except ZARDOZ) to decrypt the message and read “Molon Labe!”
Now, this is great and all, but isn’t blockchain about publicly accessible data and verification instead? Well, yes. Let’s take this public key encryption and flip it around. Now, instead of keeping the data secret, we want to make sure the data is from the right person. I’m expecting a message from ZARDOZ, and want to make sure that it’s legitimately from ZARDOZ and not from STEVE SMITH.
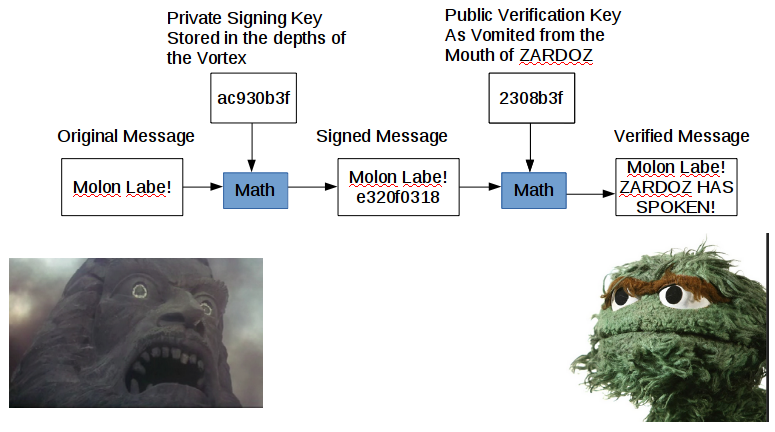
As you can see, the message stays public the entire time, but there is extra data added based on ZARDOZ’s private key. This is called a signature. Upon receipt, anybody can verify the authorship of the message by using the public key.
What happens when STEVE SMITH tries to meddle again?
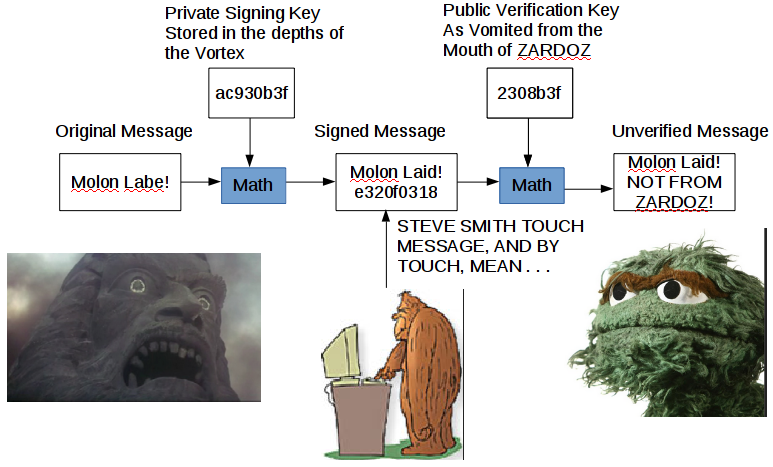
As you can see, STEVE SMITH, in his ham fisted way, has altered the message before I have received it. When I try to verify the message’s authorship, I find out that it’s not from ZARDOZ, and thus it’s a suspect message to be ignored.
This is the basis for verifying cryptocurrency transactions. We’ll put all of this book learning together into a workable model in the next article or two, but this article explains most of the theoretical underpinnings of blockchain and cryptocurrencies.

“Let’s take another break. Things are getting a bit intense. In the spirit of the glib baby pics from a while back, here’s me in a sombrero.”
CULTURAL APPROPRIATION!!!
Excellent article!
Pretty ballsy talking to the big stone head like that.
His kind and my kind have an understanding. Since we don’t procreate, ZARDOZ allows us peaceful existence in exchange for training up the brutals’ spawn to be weak and uninterested in the seed of life.
ZARDOZ SPEAKS TO YOU, HIS CHOSEN RUBBISH DWELLING ONE. AYSAY OTHINGNAY OFYAY OURYAY ECRETSAY! ZARDOZ HAS SPOKEN.
STEVE SMITH NO MESS WITH FRIEND ZARDOZ’S MESSAGES. TRSHMNSTR MAKE STEVE SMITH SAD.
…
MAYBE RAPE MESSAGES, A LITTLE.
STEVE SMITH GO BACK TO SCHOOL SO HE CAN TEACH MESSAGES NOT TO BE RAPED. AND BY TEACH, MEAN RAPE.
Sorry for the delayed reply, STEVE SMITH, I was out squatching.
Very interesting. Have you considered trying to write your own mining algorithm?
Not really. I don’t have the processing hardware to make any coin by mining, and my skills are too rusty to beat out the best and brightest by designing some super slick algorithm.
What about some of the less mature cryptocurrencies? I know Bitcoin has gotten to the point where it’s nearly impossible to mine one without a supercomputer, but some of the other ones are probably more accessible right?
I think you’re right. I may play around with the raspberry pi board over the holidays and see if I can get it mining some 3rd tier crypto. Then we can start a glib mining pool!
Or we could start our own cryptocurrency, Glibcoin, and use it to buy swag from the merch store.
I thought about suggesting such a thing, but then I remembered how lazy I am. Designing a crypto from scratch is waaaaaaaaay over my head.
Per your illustration, the currency is stored in our minds and we buy swag with it via green beams of light from our craniums?
I like it.
ITS MIND CONTROL RAYS, YOU FOOLS!
*slams foil spacehelmet on
I like titties.
You rang?
http://i.pinimg.com/736x/f0/1f/50/f01f500dd0c3f6a758e8f5686373ccb6.jpg
https://pbs.twimg.com/media/CoT9jtPUEAQxJtK.jpg
See, Trashie had the opportunity to do us a solid with pics of “Alice” “Bob(bie)” and “Eve”, but he squandered it with stale memes. Sad!
*pours one out for HM, who was obviously disemboweled by the combined forces of ZARDOZ and STEVE Smith for his insult*
STEVE SMITH seems more appropriate to model brute force attacks (AND BY BRUTE FORCE, MEAN RAPE) than man in the middle type attacks.
The pictures of Winston’s mom as the (wo)man in the middle were a little bit too NSFW for this article.
(sorry Winston, low hanging fruit and all)
+1 finger cuffs
-1 You could fit your whole arm In there.
Considering the man in the middle in this case is trying and failing to impersonate someone else, I’d have gone with tulpa; though finding a picture of him would be difficult, and also something no-one wants to see.
Ask and you shall receive
Q! ¡Eye bleach, por favor!
https://i.pinimg.com/originals/b9/9d/c5/b99dc57af6bfe1ef06bc1ac26f0b46bd.jpg
You truly are doing G-d’s work, my (((friend))).
I do what I can.
Thank you !
Distributed Rape of Service.
*applause*
Next week:
How to buy drugs on the internet
But first, a word from our sponser – the CIA, doing their part to fund violent splinter organizations since 1947.
I knew this place was too good to be true. Dangit, now I need to find another online hideaway, populated entirely by aspies, pyros, gaming geeks, high functioning sociopaths and STEVE SMITH.
ZARDOZ SPEAKS TO YOU, HIS CHOSEN MARKSMAN ONE.
…AND WHAT IS ZARDOZ, CHOPPED BRUTAL?
Wait. You’ve been real the whole time?
Does anyone else see the giant talking stone head? It would make me feel a lot better if somebody else saw the giant talking stone head.
This one?
Yeah, I saw ’em once. I ain’t ever been the same since…
Now I feel better.
I cut out the middleman and just snort raw bandwidth.
#fuckNetNeutrality
Are you going to talk about salting hashes? Bitcoin doesn’t natively include salts, and that was what allowed some of the attacks that have happened to take place. Don’t want to spoil it if you are.
I was going to describe the purpose of the nonce, but my understanding is that they’re different in purpose than salts.
There’s a shortcomings section in part 3 that I haven’t written yet, so I’ll include salts there.
I’ll have to do some research before I write that part. My pressing has been that almost all of the hacks were against the security employed by the exchanges, not against the block chain itself.
*impression
From what I’ve read the blockchains can use salts, and it was certain exchanges that didn’t use them that opened up the vulnerabilities. So the attacks were against the exchanges, but it was the lack of salting that allowed the hack.
Good news everyone! There’s a volcano forming underneath New England!
This is not news. It’s well known that most of what’s under the “Granite State” are massive batholiths. Where the hell do you think that comes from? The Northern Appalachian seismic zone is more active than one would think and is orogenic.
Yellowstone’s gonna kill us all anyway.
Progs are gonna beat Yellowstone to it..
Now you’re just making stuff up.
But what a scene, A mountain falls on Woody Harrelson!
“orogenic”
(nods knowingly, assumes its some East Asian tantric-sex thing)
Sex with a rock.
Oral sex with a rock.
It’s where ‘get yer rocks off’ originates.
HM, please tell us more about this orogenous zone.
Trump just wants to clear out New England to build more casinos.
The Earth is getting smug poisoning and is about to vomit.
Jill Stein is a Russian stooge too!
https://twitter.com/mkraju/status/943150541491834880
Oh my God- she was once complimentary toward Julian Assange! BURN THE WITCH!
I can’t even figure out who’s doing what anymore.
My initial thought was that the Trump people are encouraging this to make it look even more like a witch hunt.
But nope, there are some Hillary people who actually believe it.
You don’t understand, Russia stole the election from the most qualified candidate ever, for all time, in the history of the world, from now until the end of time. How did they do that? Well, that’s just what a Russian bot would say.
I’m starting to think you’re one of them. You cannot question the new McCarthyism. You must embrace it
OT: This from a guy who trashed his costars on Silicon Valley for not donating enough money to Hildebeast.
https://www.thedailybeast.com/silicon-valley-star-tj-miller-accused-of-sexually-assaulting-and-punching-a-woman
I guess “surprise anal” isn’t en vogue anymore.
You’ve both gotta be pretty drunk to pull off the “wrong hole” routine.
That’s the San Fansisco office.
I think that went out with Quaaludes.
his standup special on HBO is not funny at all. i was embarrassed for him by how unfunny it was. maybe my expectations were too high due to Silicon Valley.
Have you seen Trevor Noah’s “special”?
You have to try hard to be that bad.
no. i may give it a couple minutes of attention now though for the laugh (not the laugh he intended).
Who?
*confused shrug*
Don’t look at me, I have no clue.
OT: The irony! It buuuuuuurns!
https://nypost.com/2017/12/18/womens-march-organizer-accused-of-covering-up-sex-abuse/
OK, I’m a horrible person, but watch the 1 minute vid at the bottom of the page, paying attention to the woman’s tag line.
The part about… bending?
Yep: cluelessness or clever plan?
hawt
she has clay face
It’s not irony. Sansour is genuinely a horrible human being who has on several occasions admitted that she prioritizes islamic law over women’s freedom.
She tries to obfuscate it, but will admit it if questioned in such a way that allows her no wiggle room.
OT: Sucks to be consumed by the monster your ideology helped create.
http://thehill.com/homenews/media/365541-tavis-smiley-on-dating-employees-where-else-are-you-going-to-meet-people
Fear of harassment accusations was a factor in my choosing online dating.
for me it was the convenience, affordability, quality control, and pretty much every other reason imaginable over dating a co-worker.
That too.
What other mechanism is there to cheaply and frequently interact with thousands of prospective partners who share the double coincidence of wants?
It’s a no-brainer!
We didn’t have these options back when we wore onions on our belts.
bars? church? online?
who wants a church girl? They don’t even put out.
^obviously didn’t have any Catholic school friends growing up
catholic school is different.
There’s nothing like a catholic girlWith her hand in the box when she’s on her knees
Or know a Mormon girl who was away from home. I knew a couple in the Marines who were freaks with a capital F.
Mormon girls have an infinite curiosity about everything freaky.
They don’t even put out.
but when they do….
Surprise anal?
OT: Derp.
https://twitchy.com/gregp-3534/2017/12/19/hot-take-level-inferno-brianna-wu-says-super-mario-bros-is-really-about-white-colonialism/
Attention whore whores for attention, news at 11.
There’s got to be some kind of contest going on. Someone picks a random topic out of a hat, and the other person has to write a full article about how that topic is racist. It’s the only plausible explanation at this point.
On Topic: Trsh – you should take a look at Monero, my buddy is mining it using just a desktop computer. He joined a pool and has made about 25 bucks in two days. Way above price of electricity. I’m interested in joining a Glib pool if such a thing comes to fruition.
Sign me up!
Alexa Analytics for glibertarians.com:
Top Keywords from Search Engines
Which search keywords send traffic to this site?
Keyword
Percent of Search Traffic
1. glibertarian 5.78%
2. glibertarians 3.62%
3. xellenials 1.37%
4. hr 610 0.99%
5. my sex junk is so oh oh oh lyrics 0.86%
Okay… I knew we were odd, but this doesn’t even congeal properly.
4. OFFICE MANAGER MOHAMMED!!
/INFIDEL!
Please tell Mo that he forgot to file form B1-TE/M3.
Without that, his usage of capitals is limited to no more than 75% of a post.
It will need to be countersigned by STEVE before we can accept it.
ALLAH is Not pleased with the constant yelling?
There were… complaints. Our confedentiality policy prevents us from providing details of those complaints.
It was Playa! I heard him whining!
The More you know…..
🙂
Stossel does Kibbe on -isms
So here is my fundamental problem with bitcoin.
We could take the code from bitcoin, maybe tweak it a bit to make it a bit better or whatever, and create glibcoin, and keep the first million or so g$ for ourselves.
Why does bitcoin have value at $16k each (or wherever it is today) and g$ are worth 1.4 cents (if that much)? Acceptance, obviously, But they really are fundamentally the same thing. Maybe gcoins would gain acceptance and shoot up in value, but someone else could create yet another cryptocurrency and undercut us.
The block chain idea is brilliant and has a huge number of future uses, but yet another fiat currency doesnt work for me.
bitcoin is napster.
It is just a stepping stone.
So they’re going to get sued out of existance by disgruntled rich folks and the founder is going to go on to turn against their former philosophies for cash?
Meh. Every currency only has value because people want it, it’s scarce, and easily tradeable. Fiat currency requires 1. Intrinsic value, which I reject as a concept, and 2. Government dictates on its status as money. Bitcoin is lacking the second requirement, and isn’t fiat currency, and since I reject intrinsic value I see it as no different than gold. Something I have no use for except that I can trade it to someone else for something I actually want. Depending on how you view the concept of intrinsic value will change how you view bitcoin.
Bah, without intrinsic value.
Tits have intrinsic value.
I uhh, have to rethink some things… in my bunk.
They also depreciate over time.
Ha!
Q, what time is the Big reveal?
I’m gonna do it at 3 MST today, that gives people an hour into afternoon lynx to vote. I know I said 7 MST, but by that time most people are off having real lives. I’ll bump it in the lynx.
Breaking: House passes tax cuts.
https://www.nytimes.com/2017/12/19/us/politics/tax-bill-vote-republicans.html
file under: WHAT THE EVER LIVING FUCK ARE YOU TALKING ABOUT?? COLLEGE SEASON TICKETS ARE TAX DEDUCTIBLE NOW??!! obviously the poor are really going to be hit hard by this.
Darren RovellVerified account @darrenrovell
2m2 minutes ago
Tax reform bill passes house. If Senate passes & it is signed, 80% deduction to college sports season tickets goes to no deduction, starting Jan. 1. Schools would need to adjust for potential ripple, billions on line.
Stldave @StldaveS
4s4 seconds ago
Replying to @darrenrovell @moxiemom
Louisville may have to low ball players with 75K bids and hookers off of Craigslist to make ends meet
The fact that anyone could defend season tickets as a tax deduction hurts my brain.
There are probably conditions where it might count as a business expense.
well good thing business expenses already work as a write off or I would have to give a shit.
Note – I am not an accountant, and nothing I say about taxes should be taken as accurate regarding the tax code as interpreted by the Internal Revenue Service, Inland Revenue, Tax and Finance, or whatever name the taxman goes by in your area.
Eidgenössische Steuerverwaltung
That was tax-deductible!? WTF?
single mothers relied on it for childcare.
Mandatory donation to the school’s athletic fund to purchase season tickets. Like this:
http://www.rolltide.com/documents/2017/1/9//2017_TP_TAX_WEB.pdf?id=8197
Donation amount – benefit received = charitable amount that can potentially be deducted
Tickets are nominally separate and not deductible usually
The Mandatory “Donation” is not rightly considered a part of the ticket price.
If you want to donate, donate.
NOW not NOT
Indeed. But it’s (or was) a way for schools to build up their tax-deductible funds. I’m sure they’ll figure out another way to keep the money flowing into their coffers.
How high is the death toll already? Over 1000?
We’ve lost contact with the entire state of Indiana. It’s not known if there are any survivors.
Alternatively, it could be the fact that, being Indiana, no one has tried to contact them.
I can hear the gunfire from indianapolis. I think they’re alright.
Damn – I work on the fifth floor, and the pile of corpses has now reached my office window.
Is it fulfilling your Zombie fantasy?
We are fine in Indiana. But you might want to check on Illinois and California. They now have a cap on the amount of state and property tax they can deduct, which means they might realize how how high their tax rates are. The shell game is over.
“We are fine in Indiana.”
I wouldn’t go that far.
Although, I will say ‘there’s more than corn in Indiana’- there’s also Gary
Zombie Orville Redenbacher would like to have a word with you.
It takes a tough man to make a tender….no, wait, that was the other hayseed pitchman
Pssht..you’re not really from Indiana you didn’t even get the Indiana Beach reference
Oh, I got the reference. It’s just… we don’t talk about Gary.
Is their mascot still that animated crow?
So you are saying the value of my house in Phoenix is about to go way up?
That should stop gun violence in Chicago, at least.
My co-worker just dropped dead! This corporate tax cut is literally killing people somehow. Oh my God, I just saw a man outside collapse and die. Stay safe!
The Happening part 2: The Cut!
I could stare at that Ron Paul picture all day until I got a seizure from the lights.
The Ron Paul gif is people from all the seizures!
killing people*
well, I fucked that one up.
A whole school bus of children just blew-up after the House finished voting! It’s killing people! We’re dying! Somehow corporate tax cuts that bring the American tax system in line with the rest of the industrialized world is murdering people! End the madness!
We’re dying! Why Paul Ryan- why? It’s chaos! Have the staff is dead or writhing on the floor! Oh the humanity!
It’s been nice knowing you all. Who knew that having a little less money stolen from me would cause a global genocide.
*checks investments*
Nice.
*hands Just Say’n a rifle*
Don’t let them writhe like that. Help them out.
I think the DJIA may break 25000 before the end of the day.
“DJIA may break 25000”
On our blood. I just witnessed ten people die because of this bill. They’re killing us!
Yabba dabba doo!!!
I wonder how the left is going to spin this. I did hear a Dem congressman this morning complaining about how this increases the national debt. I wanted to choke the guy. But that was predictable. But on FB, will people be angry because they’ll have more money next year? They may have to get creative.
From what I’ve seen, much hay will be made of the corporate cuts being permanent while the individual cuts sunset in 10 years.
I literally just heard a lefty radio show ejit saying exactly that. “It’s going to raise taxes in 10 years!! And the deficit!!!”
Hearing lefties crowing about the deficit is too ridiculous for words.
For many years I had free healthcare through obamacare. I was selfishly happy I had it, although I fought against obamacare because I knew I was getting a free ride on the backs of others. There’s a very good chance that the progs will feel the same way about their new ‘free money’, happy they have it but guilty because they ‘stole it’ from some other ‘needier’ person.
They’ll say it cuts funding from ________. Which is fine, because the easiest retort is to explain that since they care so much about it, and since they now have more of their own money, they can simply donate it to a charity that will directly apply that money to their pet causes.
Also: “FUCK YOU CUT SPENDING”
That retort is always appropriate.
Indeed.
They’ll be happy that that have more money but it won’t be enough to offset their anger at other (bad) people having more money also.
*That they*
Pelosi’s already flogging it as “strictly for the rich” and “the worst bill to ever be on the House floor”. Some people will believe their false idols more than their own lying pocketbooks.
It’s worse than the Fugitive Slave Act! We’re all dying! I’m not sure how much longer I can go on! I just held my co-worker’s hand as she passed away! All because of that evil tax bill!
Sexual assault!!
If she died, that means she couldn’t have given consent, you rapist!
It was before she died and I had her sign a consent form first. It ain’t a joke- I am woke.
Oh my God- the building across from us just collapsed! People are dying!
Planes are falling from the skies!
Every time someone complains, reply with this:
I just realized something…you can make a credit card payment to reduce the Federal debt.
Yeah, debt to pay debt, that seems like a real good idea.
well, it worked for Lehman bros for about 150 yrs
Always good to bring in a Remmy song.
“But on FB, will people be angry because they’ll have more money next year?”
FB is the irrational outrage machine, they’ll find a way.
No joke, just before the 2008 presidential election a young woman at a bar I was at was talking about how George Bush wrecked the economy. I had no love for Bush, but I doubted that the people who said this had any cognitive point, so I asked her: “How did he wreck the economy?” First she mumbled something about regulation and I asked her what specific regulation or regulatory body did he de-regulate? She couldn’t answer so she told me that tax cuts had wrecked the economy. “How did tax cuts ruin the economy? Specifically, how did the government not taking more of our money wreck the economy?” I asked. She circled back to regulations, saying that less money for the federal government led to less funding for regulatory bodies. “When did lack of revenues ever stop the government from spending?” I asked her. She circled back to tax cuts. At his point she realized that everyone else at the bar was listening and she looked like a tremendous ass. I’m pretty sure I converted some people to voting for John McCain that night, which didn’t make me happy either. I hate everyone
This seems appropriate: https://www.youtube.com/watch?v=Y626eTivs60
In what universe could Citizens United be related to the economy?
The Rand Corporation, in conjunction with the saucer people, under the supervision of the reverse vampires, are forcing our parents to go to bed early in a fiendish plot to eliminate the meal of dinner!
The same universe where it was decided before Obama’s election?
“Welcome to Facebook! You must be at least this stupid to have an account here.”
^THIS^ ^THIS^
*furious applause*
That’s an excellent article, trashy. I might even forward it to people despite doxing myself (My real name actually is Sloopy — we just traded handles)
“Sloopy L”…hmmm, sounds like a hip-hop artist to me.
*squints*
Well done, trshmnstr! I think even OMWC could understand that.